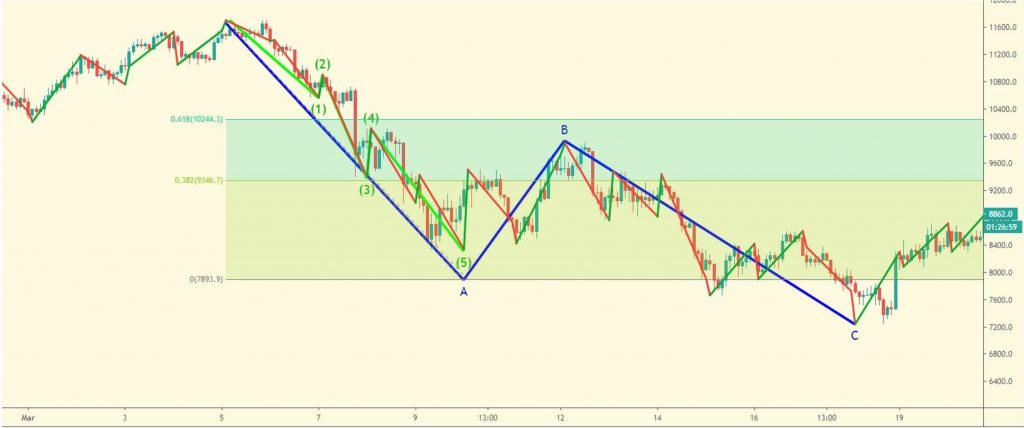
امواج الیوت به دو دسته امواج شتابدار و الگو یا امواج اصلاحی تقسیم می شوند. در آموزش کاربردی امواج الیوت به بررسی الگوهای اصلاحی بسیار پرداخته می شود. الگوهای اصلاحی خود در پنچ دسته زیگزاگ (Zigzag) ، فلت (Flat) ،مثلث (Triangle) ، دیامتریک (Diametric) و سیمتریک (Symetric) قرار می گیرند. در این مطلب در ادامه آموزش امواج الیوت به طور خاص بر روی الگوی اصلاحی زیگزاگ در سبک نئوویو متمرکز می شویم.
برای آموزش امواج الیوت کلاسیک و نحوه موج شماری به زبان ساده و مراجعه به دیگر دروس مربوط به سبک نئوویو به لینک روبرو مراجعه کنید: آموزش امواج الیوت
الگوی اصلاحی زیگزاگ (5-3-5) Zigzag
این الگو به صورت سه موج کلی است که با حروف A و B و C نام گذاری می شود. موج A و C شامل پنج ریزموج است و از نوع شتابدار می باشد و موج B شامل سه ریز موج و از نوع اصلاحی است.
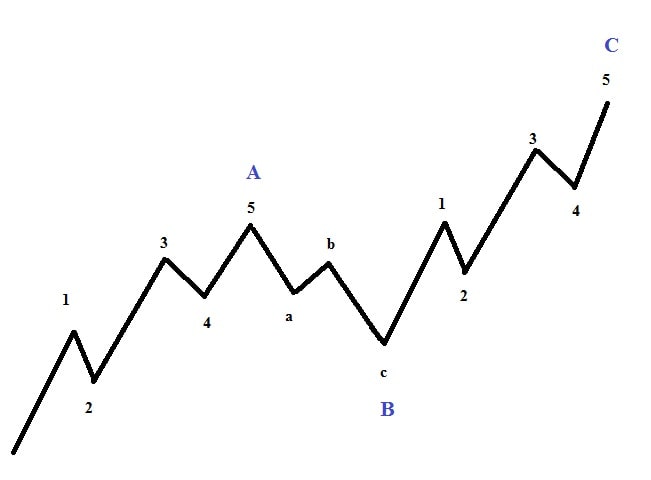
موج B از نوع امواج اصلاحی است و می تواند فرم الگوهای اصلاحی دیگر را به خود بگیرد. شرط دیگر اینست که موج C باید از انتهای موج A عبور کند.
همانطور که بیان شد موج C از نوع شتابدار (پیشرو – ایمپالس) است. امواج پیشرو خود به دو دسته رونددار و ترمینال تقسیم می شوند. اگر خط روندی ترسیم گردد که از دو نقطه صفر و B عبور کند، موج A اصلا نباید این خط را لمس کند. در صورتیکه موج C پیشرو روندار باشد این خط را لمس نمی کند. اگر چندین بار موج C این خط را لمس کرد موج B هنوز تمام نشده است.
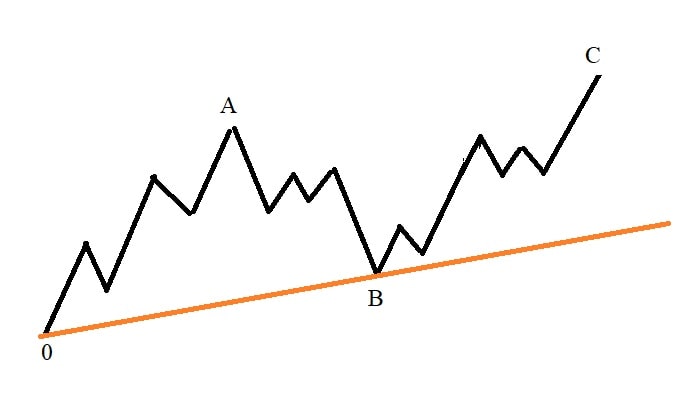
آموزش کاربردی امواج الیوت ؛ ترسیم یک کانال در الگوی زیگزاگ
خطی موازی با خط روند OB رسم شود که از نقطه A عبور کند سه حالت مختلف می تواند بوجود آید:
حالت اول: نقطه C بالای خط روند قرار گیرد
حالت دوم: نقطه C زیر خط روند قرار گیرد
حالت سوم: نقطه C روی خط روند قرار گیرد. در این حالت احتمالا با یک اصلاح پیچیده تر مواجه هستیم و این زیگزاگ بخش از آن است. (مثلا زیگزاگ دوگانه)
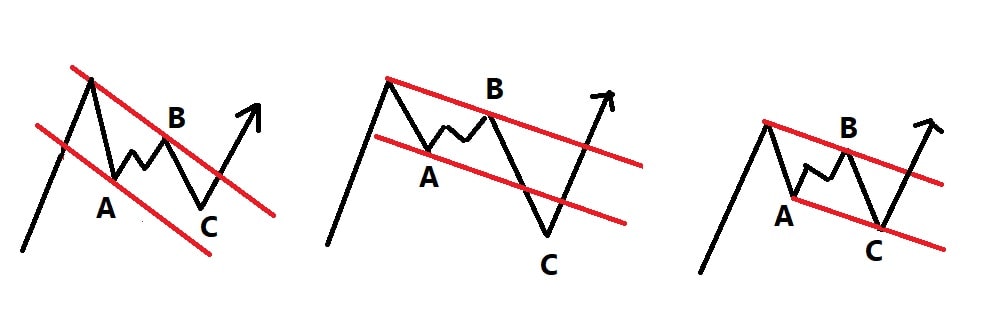
توجه شود که سه حالت فوق برای یک زیگزاگ نزولی بیان شده است. این سه حالت را برای زیگزاگ صعودی خودتان ترسیم نمایید.
شرایط دیگر
- قسمتی از موج B حداقل باید 33% از موج A را بازگردد.
- نقطه پایانی موج B (توجه شود: نقطه پایانی) از 61.8% موج A عبور نمی کند.
- هر چه موج B کوتاه تر باشد موج C قدرت بیشتری دارد.
- به لحاظ زمانی در میان سه موج A، B و C موج A بیشترین مدت زمان تشکیل را ندارد و معمولا کوتاهترین زمان را برای تشکیل خود می گیرد.
- موج B از نظر زمانی طولانی تر از موج A می شود.
- از نظر زمانی، مدت زمان تشکیل موج C بیشتر از بازه زمانی موج A و کمتر از مجموع زمان موج A وB است.
آموزش کاربردی امواج الیوت ؛ انواع الگوهای زیگزاگ کدامند؟
در آموزش کاربردی امواج الیوت الگوی اصلاحی زیگزاگ از نظر طول موج C در سه دسته قرار می گیرد.
الگوی زیگزاگ کوتاه
در این حالت موج C بین 38.2 تا 61.8 درصد موج A است. پر واضح است که روند بعد از آن بسیار قوی می باشد. در واقع کوتاه شدن موج C نشان دهنده وجود قدرت در جهت مخالف است. موج بعدی حداقل 81% کل زیگزاگ را می پوشاند. این نوع زیگزاگ به طور معمول در مثلث وسیمتریک و دیامتریک تشکیل می شود.
الگوی زیگزاگ نرمال
در این حالت موج C بین 61.8 تا 161.8 درصد موج A است.
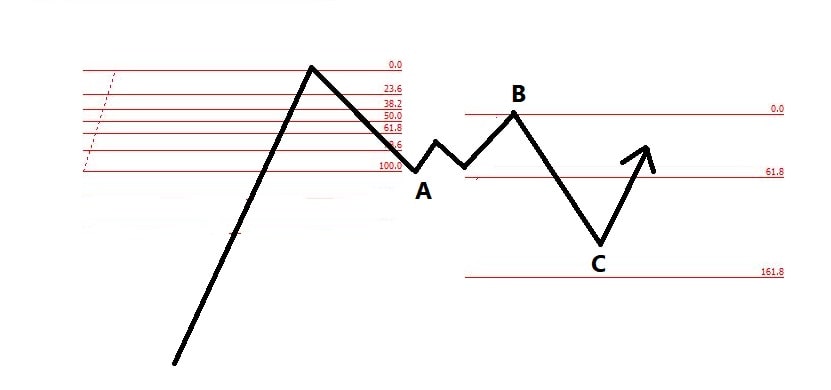
در فوق یک فیبوناچی از ابتدا تا انتهای موج A زده شده تا فاصله قیمتی طی شده بدست آید بعد همان فیبو روی ابتدای موج C کپی شده است. انتهای موج C در محدوده 61.8 تا 161.8 درصد موج A است.
الگوی زیگزاگ ممتد یا کشیده
در این حالت موج C بیشتر از 161.8 درصد موج A امتداد می یابد و معمولا تا قبل از رسیدن به 261.8% موج A به پایان می رسد. این نوع زیگزاگ معمولا در مثلث و دیامتریک و سیمتریک تشکیل می شود. موج بعدی بایستی حداقل 61.8% از موج C را اصلاح کند.
گرفتن تاییدیه پس از الگوی زیگزاگ
گرفتن تاییدیه از اصول سبک نئوویو در آموزش کاربردی امواج الیوت است و در آموزش کاربردی امواج الیوت براین نکته بسیار تاکید می گردد. در این الگو گرفتن تاییدیه شامل دو گام می شود.
گام اول: شکسته شدن خط روند OB
پس از اینکه تحلیلگر به این نتیجه رسید که موج C به پایان رسیده است، بایستی موج بعدی خط روند OB را در زمان کمتری نسبت به بازه زمانی موج C بشکند. در غیر اینصورت موج C هنوز تمام نشده است. شاید موج C دارد ساختار موج پیشرو ترمینال به خود میگیرد و یا اینکه ریزموج چهارم موج C در حال تکمیل شدن می باشد.
گام دوم: زمان پوشش موج C
همانند گام اول وقتی چارتیست یا تحلیلگر بر اساس موج شماری خود نتیجه گرفت که موج C به کار خود پایان داده است، موج بعدی باید کل موج C را در مدت زمان کمتری نسبت به بازه زمانی تشکیل موج C بازگردد. وگرنه موج C هنوز موج شماری باید اصلاح شود.
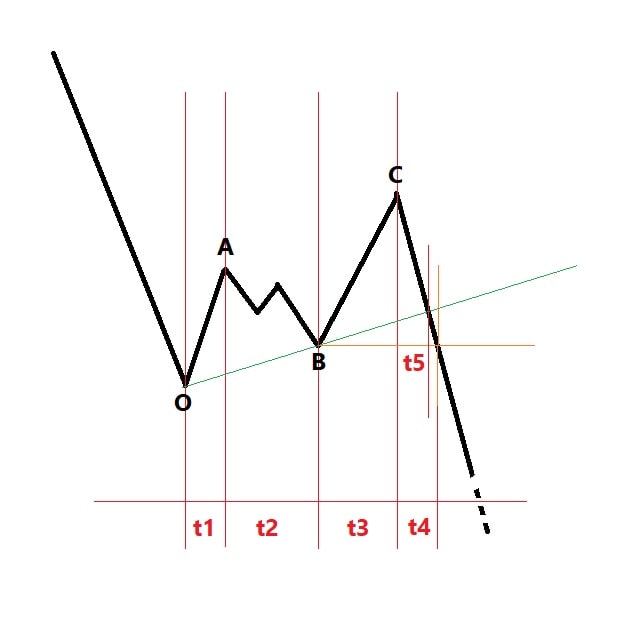
به طور کلی در الگوی اصلاحی زیگزاگ روابط زمانی زیر بایستی برقرار باشد:
t2>=t1 , t3>=t1 , t3>=t5 , t3>=t4
منابع:
- کتاب آقای ناصر دادگستر
- آموزش های آقای محمد محبی
- https://www.liteforex.com/blog/for-professionals/neowave-part-16-extended-rules-of-logic-for-zigzags-and-flat-corrections/